GGP 4. Input Assembler & Vertex Processing(2)

지난 포스팅에서 Vertex shader에는 4가지 world와 3가지 transform이 있는 것을 배웠다. 이번 포스팅에서는 camera space에서 clip space로 가는 projection transform에 대해 다루겠다.

 

View Frustum

카메라는 모든 물체들을 다 보지는 못한다. 씬에서 보이는 영역들을 view frustum이라고 부른다.

view frustum은 잘린 피라미드 모양이며, aspect(w/h), fovy(y축 방향의 시야 정의), n, f등 파라미터들로 정의된다. n은 near plane, f는 far plane이다.

 

• View frustum culling: 각 물체를 감싸는 bounding box를 만들고, 이 object 자체가 view frustum에 들어가는지를 검사한다. 만약 들어가지 않으면 아예 오브젝트의 정보 자체를 GPU에 안보내고 버린다. GPU의 연산 파워를 아낄 수 있다.
• Clipping: view frustum과 polygon이 겹치는 경우, view frustum안에 들어온 부분만 처리되고 바깥 부분은 잘라버린다. 이 과정은 rasterization단계에서 이루어진다. 위 사진에서 view frustum과 겹친 오브젝트에서 빨간색으로 표시된 부분을 자른다. 근데 자르면, 그 단면에서 새로운 vertex들이 생기고 만들어야 되기에 GPU 부하가 올 수 있다. 그러나 이들을 일일이 나중에 라이팅하고 색입히며 필요없는 것들을 하는 것보다는 차라리 이게낫다~~
• 둘다 GPU에서 처리된다.

Projection Transform

앞에 그림에서는 view frustum 을 사각뿔대 모양의 절두체로 표현하였지만, 실제로는 원점이 중심인 2x2x1 사이즈의 직육면체(clip space)로 변환한 후에 clipping한다. [-1, 1] x [-1, 1] x [0, 1] 의 좌표를 가진다. 이렇게 잘린 피라미드 모양의 절두체를 직육면체로 변환하는 것이 projection transform이다. 카메라 스페이스의 물체들은 projection transform 된 후에 직육면체(clip space)에 대해 clipping을 거친다. 이런 projection-transformed objects는 clip space에 있다고 표현한다. 그 후에 clip space에 있는 정보를 2D space에 올린다. clip space는 실제 물리적 공간이라기 보다,  3D좌표를 2d화면에 투영하게 해주는 수학적으로 정의된 공간이라고 보면 된다.

 

위의 사진을 보자. 왼쪽 그림에서 선들이 모이는 점이 원점, 즉 카메라의 위치(EYE)이다. 모든 projection line의 3D 점들은 투영된 이미지의 2D점들에 매핑된다. 이때, 실제로는 l1>l2이지만, clip space에선s l1 = l2로 보인다. 따라서 더 멀리있는 애는 실제보다 더 작게보이고, 가까이 있는애는 실제보다 크게 보이는 이런 원근감이 나타난다.  projection line은 z축과 평행하게 된다.

Orthogonal transform: 크기를 왜곡하지 않음, 기술 도면 및 설계,UI 렌더링,수학 이론등 정확한 치수와 비율을 유지할때 쓰임
Projection transform: 실제로 우리가 보는 눈의 관점,센서로부터 주변 상황 인지할 때(ex 레이저를 쏠때), 데이터를 얻어야 하는데 내가 존재하는 영역 대비 캡쳐해야 하는 영역이 크면 perspective transformation을 통해 차원을 압축해 다룰 수 있음

---

Projection Transform matrix는 어떻게 도출할까?

 

최종목표는, 원래 좌표였던 v = (x, y, z,1)을 v' = (x', y', z', 1)로 바꾸는 것이다.

일단 2D에서 먼저 보자. projection matrix는 view frustum을 2x2x1사이즈의 큐브로 바꿔준다. 2d에서의 v좌표를 (y,z)라고 쓰고, 이를 projection 한 곳이 v'(y', z')이다. projection 평면은 z축과 수직이다. 만약 v'의 z좌표가 cot fovy/2라면 y좌표는 -1~1이기에, 닮음을 이용하면, y:z = y' : cot fovy/2, y' = y/z * cot fovy/2이다. 마찬가지로 x' = x/z * cot fovx/2로 표현할 수 있다.

 

이제 3D로 확장하자.

aspect = W/H이고, 그림에서 H = D * tan fovy/2, W = D * tan fovx/2 이다. aspect는 정리하면 위의 식과 같이나온다. 이를 이항하여 cot fovx/ 2 = (cot fovy/2)/aspect로 나타낼 수 있다. 그러면 다시 최종 목표인 x', y'를 원래 x,y를 이용해 나타내보자. 위의 2D일때 구했던 식을 이용한 후 , cot fovx/2대신 (cot fovy/2)/aspect를 써준다. cot fovy/2를 D, aspect를 A로 치환하면, 위의 식과 같이 변환됨을 확인할 수 있다.

 

---

앞의 수식에서 x' , y'는 모두 x,y를 이용해 나타내었지만, z'는 zz'로 나타내었다. 이 z'를 다시 z로만 나타내보자. 우선, zz'를 편의상 z''라고 표현하겠다.

 

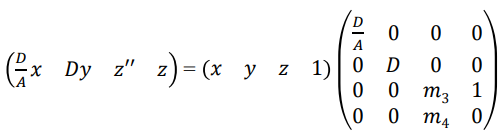
새로 구한 행렬을 원래 행렬과 구하고자 하는 projection matrix의 곱으로 나타내보았다. 우리는 z에 무엇을 곱해야 z''가 되는지 궁금하기에, projection matrix의 3열을 미지수인 0,0,m3,m4로 채웠다. 3열 1행, 2행을 0으로 채운 이유는 z축의 좌표는 x,y축과는 무관하기때문이다.

행렬 계산을 해보면 다음과 같다.

따라서 z' = m3 + m4/z로 표현할 수 있다. 그런데 미지수는 m3,m4 똑같이 2개이므로 미지수를 줄이고 싶다.

 

우리는 projection transform을 하고 나면, near plane은 z = 0으로, far plane 은 z= 1로 대응됨을 알고있다. 이를 위의 z' = m3 + m4/z에 대입해 식 두개를 도출할 수 있다.

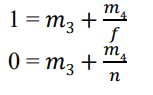
이것을 연립하여 m3와 m4의 값을 구하면 다음과 같다.

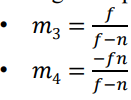
이를 다시 대입해서, 최종적으로 구한 projection matrix는 다음과 같다. 다시 D = cot fovy/2, A = aspect로 되돌려주면, 결국 fovy, w, h ,f, n로 matrix가 결정됨을 알 수 있다.

 

---

Right-hand System vs Left-hand System

3D공간에서 좌표축을 결정할때는 RHS또는 LHS를 사용한다.

• RHS: 오른손 좌표계.  x축 -> y축 방향으로 오른손의 검지~새끼 손가락을 감았을때, 엄지손가락이 향하는 방향이 z축(ex OpenGL)
• LHS: 왼손 좌표계.  x축 -> y축 방향으로 왼손의 검지~새끼 손가락을 감았을때, 엄지손가락이 향하는 방향이 z축(ex Direct3D)

 

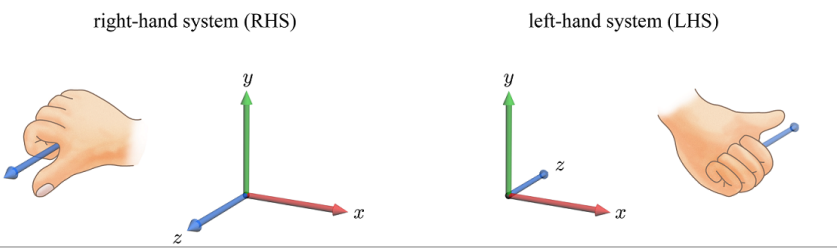
예시를 들어보자!

EYE = (0,0,0), AT = (0,0,-1)인 상황, 카메라가 이미지를 캡쳐한다.

그런데 같은 상황을 LHS에서 본다면, 아래 그림과 같이 그림이 좌우반전되어서 나타난다.

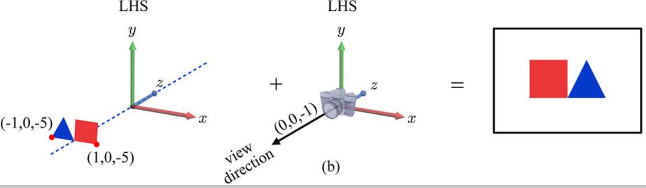
이런 현상을 막기 위해서는, RHS에서 LHS로 전환할때, z축 부호를 뒤집어야 한다.

위 그림에서처럼, LHS일때는 z축의 좌표를 -5,-5,-1이 아니라 5,5,1로 뒤집어야 똑같이 나오는 것을 확인할 수 있다.

 

또한, Direct3D(LHS)에서는 2X2X1 사이즈의 큐브로 view frustum을 바꿨지만, OpenGL(RHS)에서는 2X2X2사이즈의 큐브로 바꾼다. 따라서 위의 두 가지 이유때문에, OpenGL에서의 projection transform matrix는 달라질 수 밖에 없다.

 

위에서 구했던 방법과 동일한 방법으로 구하나, z축이 뒤집어졌기에 -부호가 붙고, 2x2x2사이즈이기 때문에 near plane(-n)일때는 z = 1, far plane(-f)일때는 z =- 1이다.

z대신 -z가 들어간것을 알 수 있다.

OpenGL은 열벡터 표기법으로, 구하고자 하는 matrix가 벡터 앞에 곱해진다. (Direct3D는 행벡터 표기법, matrix가 벡터 뒤에 곱해진다)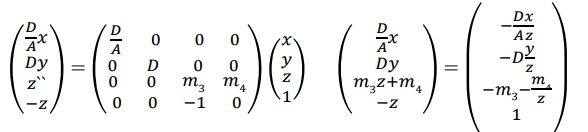

-z로 나눠준다. - > z' = -m3 -m4/z

최종 projection transform matrix!